السلام عليكم
نظرية الساندوتشهذه النظرية من النظريات المفيدة في النهايات ويعتمد عليها في تعيين النهاية لدالة ذات علاقة بين دالتين أخريين على نفس الفترة.
ويطلق على هذه النظرية نظرية الساندوتش Sandwich Theorem أو نظرية الكبس أو القرص أو الحصار (Squeez Theorem) or (Pinching Theorem) or (Squeezing Principle). ويطلق عليها في إيطاليا
"Teorema dei due carabinieri" وسميت بذلك لأنها تصف نهاية دالة محاصرة بين دالتين. فهيئتها حينئذ كهيئة (شاطر ومشطور وبينهما كامخ)

'>
وقبل أن ندخل في النظرية لنتصور هذا المثال:
إذا كان لديك ثلاث طرق. بحيث يكون الطريق الأوسط - على امتداده- دائما في وضع وسط بين الطريقين الآخرين.
فماذا تتوقع إذا قلت لك أن الطريقين الطرفيين يلتقيان عند نقطة؟؟؟؟؟؟؟؟؟؟؟؟
نعم هذا صحيح...... ما دام الطريق الأوسط يتوسط الطريقين دائما، وبما أن الطريقين التقيا.. فإنه سوف يمر الطريق الأوسط بنقطة التقاطع هذه.
وهذا هو بالضبط ما تحكيه النظرية عن الدوال!
نص النظريةif
\le g(x)\le h(x))
when x is near a (exept possibly at a) and
 ={\lim }\limits_{x \to a} h(x) = L)
Then
 = L)
إذا كان
\le g(x)\le h(x))
عندما x قريبة من a، وكان
 ={\lim }\limits_{x \to a} h(x) = L)
إذن
 = L)
والشكل التالي يوضح هذه النظرية
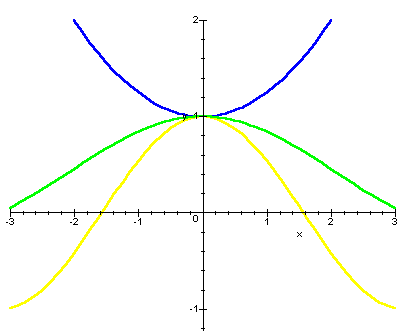
إذا نظرنا للرسم فسنجد أن الجراف الأخضر هي دالة تتوسط دالتي الجرافين الأزرق والأصفر..أي أنه على الفترة الممتدة يكون أكبر من الأصفر وأصغر من الأزرق!. ثم حدث أن نهاية الأزرق والأصفر تساوتا عند x=0 بحيث النهاية تساوي 1. إذن فإن نهاية دالة الجراف الأخضر تساوي 1.
وانظر كذلك إلى الشكل التالي
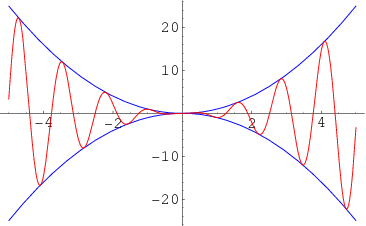
الدالة المبينة باللون الأحمر أكبر من الدالة الزرقاء السفلية وأصغر من الدالة الزرقاء العلوية... وعندما التقت الدالتان الزرقاوان في النهاية عند x=0 التقت معهما الدالة الحمراء
وسنؤجل البرهان بإذن الله إلى ما بعد الأمثلة!!!
والسلام عليكم ورحمة الله وبركاته

'>